В завершающие месяцы 2025 года президент США Дональд Трамп анонсировал планы по организации государственного софинансирования для фирм, работающих над квантовыми компьютерами. Этот подход аналогичен тому, что ранее в том же году было применено к корпорации Intel, когда правительство приобрело в ней миноритарный пакет акций. Поддержка нацелена на ведущие компании в данной сфере, такие как IonQ, Rigetti Computing, D-Wave Quantum, Quantum Computing и Atom Computing. В большинстве своём эти компании восприняли инициативу позитивно, поскольку передовые исследования в IT-области требуют масштабных и долгосрочных вложений с неочевидной окупаемостью, а разработка полноценных квантовых систем — задача особенно капиталоёмкая. Помимо сложностей с созданием и поддержанием квантовой запутанности между большим числом кубитов, критически важной задачей остаётся эффективное исправление ошибок, неизбежно возникающих в процессе вычислений. Ранее мы уже анализировали один из методов коррекции — низкоплотную проверку чётности, предложенную IBM. Теперь же стоит обратить внимание на альтернативные подходы, разрабатываемые другими научными группами.
Художественное изображение логического вентиля, реализующего квантовую запутанность (источник: University of Sydney)
⇡#Тревоги Розетты
В конце XVIII столетия в Египте был найден объект, который стал ключом к пониманию иероглифической письменности — Розеттский камень. На нём один и тот же текст был нанесён тремя способами: древнеегипетскими иероглифами, более поздним демотическим письмом и на древнегреческом языке. С того времени в науке и технике «розеттскими камнями» начали называть открытия, которые благодаря удачной аналогии позволяют осмыслить, а затем, разобравшись в сути, и воссоздать нечто прежде недоступное. Именно так, «розеттским камнем квантовых вычислений», был назван квантовый логический вентиль, представленный в августе 2025 года учёными из Лаборатории квантового контроля Наноинститута Сиднейского университета. Причина в том, что он теоретически даёт возможность кардинально уменьшить количество физических кубитов, требуемых для формирования одного логического кубита. Напомним, что как раз к 2026 году компания IBM планирует запустить 12-кубитный квантовый компьютер, построенный на 288 физических трансмонных кубитах и выполняющий вычисления с погрешностью не выше 0,1%. Это означает, что для реализации каждого логического кубита здесь используется 24 физических, объединённых в сложную схему коррекции ошибок. И такой результат по праву считается значительным достижением: если бы аналогичный вычислитель создавался на основе поверхностного кода для исправления ошибок (как, например, в квантовых процессорах Google серии Willow), то для формирования тех же двенадцати логических кубитов с сопоставимой точностью потребовалось бы уже около 3 тысяч физических — то есть на порядок больше.
Подобно классическим схемам, квантовый вычислительный контур формируется из ряда логических элементов, соединённых в заданной последовательности; именно прохождение сигналов через эту цепочку и осуществляет вычисления. Если абстрагироваться от физической реализации, каждый элемент можно рассматривать как оператор, преобразующий входные сигналы в выходные согласно определённым правилам (здесь стоит отметить, что число входов и выходов у квантовых элементов должно быть одинаковым в силу требования унитарности). В квантовых вычислениях в роли сигналов выступают состояния конкретных кубитов, задействованных в процессе. Однако на всех этапах вычислений кубиты должны сохранять свою квантовую природу, то есть оставаться в состоянии суперпозиции, не коллапсируя в базовые состояния |0⟩ или |1⟩. Поэтому квантовые элементы, выполняющие операции с двумя и более кубитами, обязаны запутывать эти кубиты (entangling logic gates) — создавая квантовые корреляции между ними, так чтобы измерение состояния одного из запутанных кубитов мгновенно определяло состояние другого. Классический пример запутывающего элемента — управляемый инвертор (controlled NOT; CNOT): он оперирует двумя кубитами — управляющим и целевым. Если управляющий кубит коллапсирует в состояние |1⟩, то целевой немедленно принимает состояние, противоположное своему исходному, каким бы оно ни было. Ещё раз подчеркнём, что все операции внутри квантового контура, пока он пребывает в состоянии суперпозиции, полностью обратимы, поэтому утверждение, будто CNOT «изменяет состояние целевого кубита на противоположное», не совсем точно: в конечном счёте изменение произойдёт, но до момента разрешения квантовой неопределённости, в состоянии суперпозиции запутанной системы, скрыты все потенциально возможные исходы.
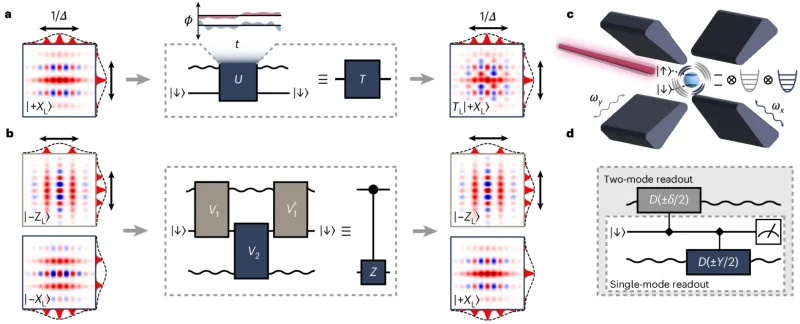
Иллюстрация из обсуждаемой статьи в Nature Physics, на которой показаны: реализация однокубитного (a) и двухкубитного (b) вентилей на захваченном в ловушку ионе иттербия (c), а также схема проведения одно- и двухмодовых измерений по протоколу GKP (d) (источник: University of Sydney)
Идея запутывающего квантового элемента, разработанного учёными из Сиднея, заключается в реализации протокола Готтесмана – Китаева – Прескилла (Gottesman – Kitaev – Preskill code; GKP). Этот протокол, названный в честь Дэниела Готтесмана, Алексея Китаева и Джона Прескилла, был впервые описан в их работе 2001 года. Сравнение GKP с Розеттским камнем уместно, поскольку данный метод позволяет точно представлять кубиты — а точнее, любые квантовые системы с конечной размерностью гильбертова пространства — в другой квантовой системе, например, с помощью осцилляторов. Образно говоря, он выполняет перевод с древнеегипетской иероглифической записи на классический греческий, полностью сохраняя исходное закодированное сообщение. Основу протокола составляют так называемые решётчатые состояния, которые остаются неизменными при сдвиге на определённую величину: эта повторяющаяся структура позволяет легко обнаруживать и корректировать небольшие ошибки, возникающие при смещении состояний кубита. Таким образом, одно правильно сконструированное решётчатое состояние — то есть соответствующим образом подобранный оператор смещения — заменяет целый набор контрольных кубитов, которые пришлось бы запутывать с исходным для постоянного мониторинга его состояния. Однако в данном случае отказ от физической избыточности в количестве требуемых кубитов (для реализации всего одного логического) достигается за счёт создания достаточно сложной системы, способной хранить информацию об осцилляциях (колебательных состояниях) кубитов — с использованием бозонных кодов. Другими словами, не каждая квантовая система поддаётся коррекции с помощью GKP, да и сам протокол способен исправлять не любые ошибки, а лишь относительно малые.
Учёные из Сиднейского университета использовали ловушку Пауля для удержания одиночного иона иттербия, чьё энергетическое состояние обладает собственным спектром колебаний, возникающим благодаря взаимодействию внутреннего электромагнитного поля частицы с внешним удерживающим полем. Этот спектр является дискретным, что даёт возможность закодировать сначала один кубит по протоколу GKP в получившемся гармоническом осцилляторе, а затем и второй: поскольку ион колеблется в трёхмерном пространстве, его смещение по каждой из осей можно трактовать как независимое квантовое состояние, а так как ион един — колебания по двум направлениям оказываются изначально запутанными. В квантовой теории гармонические осцилляторы и бозоны (частицы, подчиняющиеся статистике Бозе — Эйнштейна) описываются аналогичными операторами, поэтому подобные методы обработки квантовой информации — использующие бесконечномерные гильбертовы пространства гармонических осцилляторов для кодирования логических кубитов с коррекцией ошибок — принято называть бозонными. Помимо механических колебаний захваченных ионов, на которые ориентировалась сиднейская группа, бозонные схемы можно реализовать, например, на электромагнитных модах в микроволновых резонаторах или на оптических фотонах. Однако специфика такого подхода, связанная с применением гармонических осцилляторов, осложняет создание универсального набора квантовых вентилей в рамках протокола GKP. Поэтому даже если экспериментальная установка учёных со временем превратится в функционирующий квантовый компьютер, спектр задач, которые в принципе можно на нём решить, окажется ещё уже, чем тот, что теоретически доступен для квантовых алгоритмов. Вместе с тем, важное преимущество предложенного метода — отсутствие потребности в криогенном охлаждении системы: ион иттербия удерживается в ловушке Пауля лазерами при обычной комнатной температуре.

Ловушка Пауля — это набор электродов, расположенных внутри вакуумной камеры, показанной на изображении. Если размеры всего одного вентиля будущего квантового компьютера (не требующего дополнительных корректирующих кубитов) окажутся столь значительными, то полноценная система, способная решать практические задачи и содержащая около тысячи логических кубитов, станет поистине гигантской (источник: Wikimedia Commons)
⇡#Это просто магия!
Квантовые эффекты фундаментально отличаются от явлений макроскопического мира, которые мы воспринимаем непосредственно: достаточно вспомнить нелокальность квантовой запутанности, то есть мгновенное (не ограниченное скоростью света, а моментальное) изменение состояния одного из пары заранее запутанных квантовых объектов в тот самый момент, когда измеряется состояние второго, — независимо от расстояния между ними. Именно поэтому моделирование квантовых вычислений на классических компьютерах не только сложно, но — после определённого уровня — принципиально неточно: алгоритмически полноценно запрограммировать физически корректное поведение квантовых эффектов в действительно сложных системах оказывается невозможным. Теперь становится ясно, почему, описывая наиболее многообещающие квантовые компьютеры, учёные упоминают волшебные состояния (magic states). Это особые конфигурации квантовых систем, которые принципиально невоспроизводимы классическими методами, — и именно благодаря им, как ожидается, в будущем будет достигнуто квантовое превосходство над любыми, даже самыми сложными, полупроводниковыми вычислительными системами.
Ранее рассмотренный вентиль CNOT, детально описанный в прошлой статье поверхностный код для квантовой коррекции ошибок, а также множество других операций, активно используемых создателями квантовых компьютеров, входят в категорию клиффордовых вентилей (Clifford gates). С одной стороны, они эффективны для выполнения ключевых квантово-вычислительных задач, таких как запутывание кубитов или исправление ошибок. С другой — при ближайшем рассмотрении их нельзя назвать в полной мере квантовыми. Дело в том, что эти элементы настолько успешно упрощают — лишают загадочности и неочевидных аналогий с макроскопическими явлениями — взаимодействие квантовых частиц, что операции с их участием отлично моделируются обычными классическими машинами. Пусть и с колоссальными затратами времени, энергии и вычислительных мощностей; однако квантовое преимущество клиффордовых схем (Clifford circuits) над традиционными полупроводниковыми системами — сугубо количественное, да и то не слишком значительное. Формально здесь нет обмана: аппаратные клиффордовые вычислители действительно проводят квантовые операции над реальными кубитами и дают результат гораздо быстрее, чем при решении той же задачи на классическом компьютере. Тем не менее, фундаментальная теорема Готтесмана–Книлла (Gottesman-Knill theorem) утверждает, что любое квантовое вычисление, построенное исключительно из клиффордовых операций, может быть выполнено и на классическом компьютере — за полиномиальное время. Иначе говоря, опора лишь на клиффордовы вентили позволяет создать лишь необратимый квантовый компьютер — в определённом смысле аналог классического, где жёстко задана стрела времени; задана самим предположением, что вычисления могут порождать ошибки, которые, в свою очередь, можно исправлять, по сути возвращая систему в предыдущее состояние для повторного расчёта. Однако на квантовом уровне процессы полностью симметричны относительно направления течения времени; следовательно, универсальный квантовый вычислитель, как мы уже неоднократно отмечали, должен быть абсолютно обратим — до тех пор, пока не получен конкретный результат, то есть пока не произошёл коллапс волновой функции.
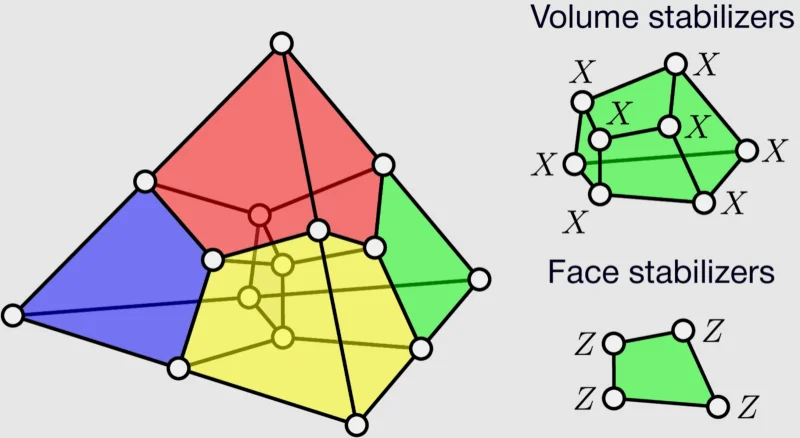
Визуализация квантового кода Рида-Мюллера (Reed-Muller code), где 15 физических кубитов объединяются в один логический кубит с дистанцией 3 (distance-3, или d3 — что означает способность выявлять и корректировать одну ошибку). Данный код является самым компактным d3-кодом, пригодным для реализации неклиффордова T-гейта, и наиболее широко применяется в процедуре дистилляции магических состояний (источник: arxiv.org/abs/2507.12511)
В чём же заключается недостаток клиффордовых вентилей? Допустим, их программная эмуляция на классическом компьютере будет решать определённую задачу десятилетиями, в то время как реальный 1000-кубитный квантовый процессор справится за несколько месяцев (а не за считанные минуты, как в случае экспоненциального, а не полиномиального ускорения). Так есть ли принципиальная разница, является ли он универсальным? Для специалистов, чьи интересы напрямую связаны с решаемой проблемой (например, для криптографов, которым всё равно предстоит отказываться от RSA), эта разница может показаться несущественной. Однако спектр алгоритмов, эффективно выполняемых на клиффордовых компьютерах, довольно ограничен — и, что самое важное, крайне желательно достичь экспоненциального ускорения там, где его пока нет. Давайте вспомним, что подразумевается под универсальным многокубитным квантовым компьютером: если количество кубитов в состоянии суперпозиции равно L, то общее число линейно независимых состояний такой системы составляет 2L. По сути, весь вычислительный процесс сводится к одному-единственному повороту вектора состояния в гильбертовом пространстве размерности 2L. Для реализации такого поворота необходимо свободно манипулировать состояниями запутанных кубитов. И если S-вентиль (фазовый вентиль), который поворачивает вектор состояния отдельного кубита на сфере Блоха на 90° вокруг оси Z, относится к клиффордовым, то T-вентиль, осуществляющий поворот лишь на 45°, — уже нет. Физически реализовать T-вентиль вполне достижимо, но возникает сложность: для него невозможно создать столь же надёжную (пусть и сложную) систему коррекции ошибок, как для клиффордовых вентилей. Он принадлежит к другому классу!
Более двадцати лет назад Эмануэль Книлл, соавтор знаменитой теоремы Готтесмана-Книлла и ключевая фигура в современной теории квантовых вычислений, предложил концепцию постселективных квантовых вычислений. Идея заключалась в создании фильтрующей схемы — естественно, также квантовой и органично встраиваемой в компьютер, — которая пропускала бы выходные данные (включая прошедшие через зашумлённые элементы) для последующей обработки лишь при соответствии результатов измерений определённым заранее критериям. В роли такого фильтра должны были выступать вспомогательные кубиты, подготовленные в особое — так называемое магическое состояние (magic state). При передаче этого состояния через клиффордов вентиль результат оказывается идентичным выполнению неклиффордовой операции (например, T-вращения). Вследствие этого вся система возвращается в рамки клиффордовой (правда, практические методы создания устойчивых магических логических кубитов Книлл не детализировал), что снова позволяет применять алгоритмы коррекции ошибок. При этом вычислительное преимущество системы над классическим фон-неймановским компьютером становится ближе к экспоненциальному, нежели к полиномиальному. Именно «ближе», поскольку необходимость исправлять обнаруженные ошибки всё же замедляет процесс, но такой шаг, безусловно, представляет собой значительный прогресс.

Устройство для дистилляции магических состояний, созданное на платформе квантового компьютера Gemini, в котором кубиты реализованы на нейтральных атомах (источник: QuEra)